Measurement of Inductance and Capacitance
AC Bridge
The bridge is used for the measurement of electrical quantities such as inductance, capacitance and resistance. AC bridges help us find out the storage factor, loss factor and dissipation factor when used in the circuits.
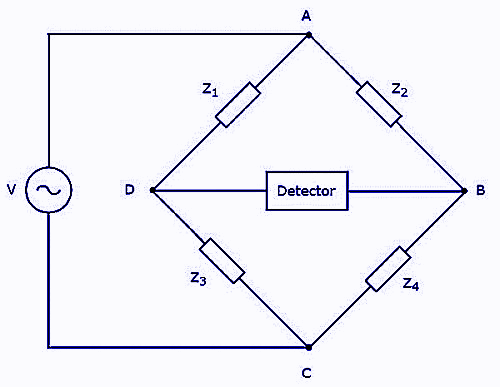
The circuit diagram of the AC bridge is similar to that of the DC bridge. The above AC bridge has four arms and each arm consists of some impedance. That means each arm will have either a single or combination of elements such as resistor, inductor and capacitor. Out of the four impedances two of them have a fixed value, the third one has a variable value and the fourth has an unknown value which can easily be measured using AC bridges.
Maxwell’s Bridge
Maxwell’s bridge is a modification to a Wheatstone bridge used to measure inductance. The measured inductance can be in terms of calibrated resistance and inductance or resistance and capacitance. The working principle of Maxwell’s bridge is that the positive phase angle of an inductive impedance can be compensated by the negative phase angle of a capacitive impedance when put in the opposite arm and the circuit is at resonance; i.e., no potential difference across the detector and hence no current flows through it.
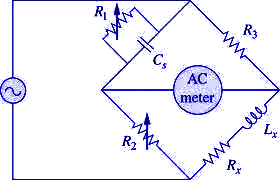
Here,
LX or L = Unknown Inductance
R4 or Rx = Effective resistance of inductance coil
R1 , R2 , R3 = Known resistances
C1 = Standard Variable Capacitor
The balanced equation of each branch can be written as:
Equating the real and imaginary parts,
There are two types of Maxwell bridges:
- Maxwell’s Inductance bridge where only inductors and resistors are used.
- Maxwell’s Inductance and Capacitance bridge where inductors, capacitors and resistors are used.
Advantages of Maxwell’s Bridge
The balanced equations are independent of the frequency factor and hence can be solved independently.
Disadvantages of Maxwell’s Bridge
In the setup of Maxwell’s bridge, a variable capacitor is used which is very expensive. Also, the bridge is limited to low quality inductor coils and is unsuitable for low quality Q factor value (Q < 1).
Bhopal, MP, 462004




