CFG stands for Context Free Grammar. It is a formal grammar which finds possible patterns of strings in a given formal language. This is an excellent tool for translating certain languages into different dialects. We can make use of this CFG as a part of translating programming languages as well. Necessity of using this tool is because of random input strings. These input strings contain information which is not understandable by machine. As a result, to translate it into machine convenient language we can use it.

Context Free Grammar and Working Concept
A CFG is a 4-tuple such that-V =
Finite non-empty set of variables and non-terminal symbols
T = Finite set of terminal symbols
P = Finite non-empty set of production rules and of the form A → α where A ∈ V and α ∈ (V ∪ T)*
S = Start symbol
Why CFG is call so?
CFG provides no mechanism to restrict the usage of the production rule A → α within some specific context unlike other types of grammars.
That is why it is called as “Context Free” Grammar.
Example-01:
Consider a grammar G = (V , T , P , S) where-
V = { S }
T = { a , b }
P = { S → aSbS , S → bSaS , S → ∈ }
S = { S }
As a result, these languages are close under union.
CFGs are close under concatenation.
These’s CFGs are close and under kleen closure.
Because Languages are not close and under intersection and complement.
Family of regular language is a proper subset and of the family of context free language.
Each Context Free Language is accepting by a Pushdown automaton.
Ambiguity in Context Free Grammar-
A grammar is said to be ambiguous if for a given string generated by the grammar. As a result, there exists more than one leftmost derivation and more than one rightmost derivation or more than one parse tree (or derivation tree).

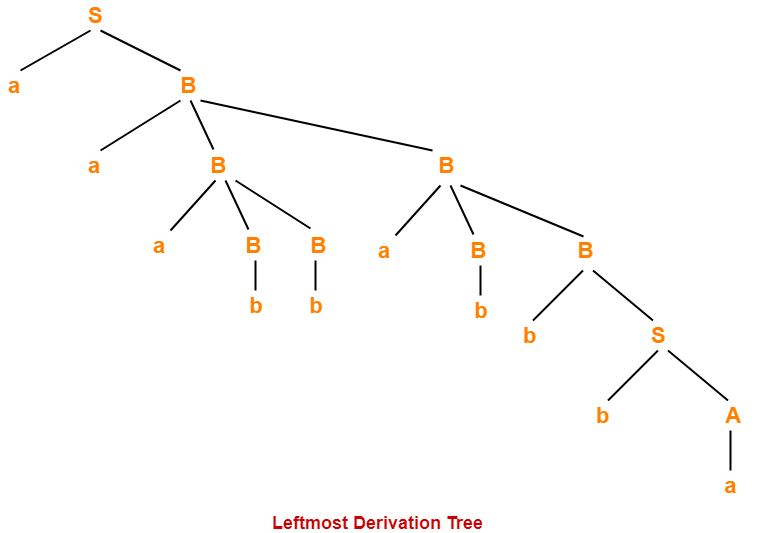
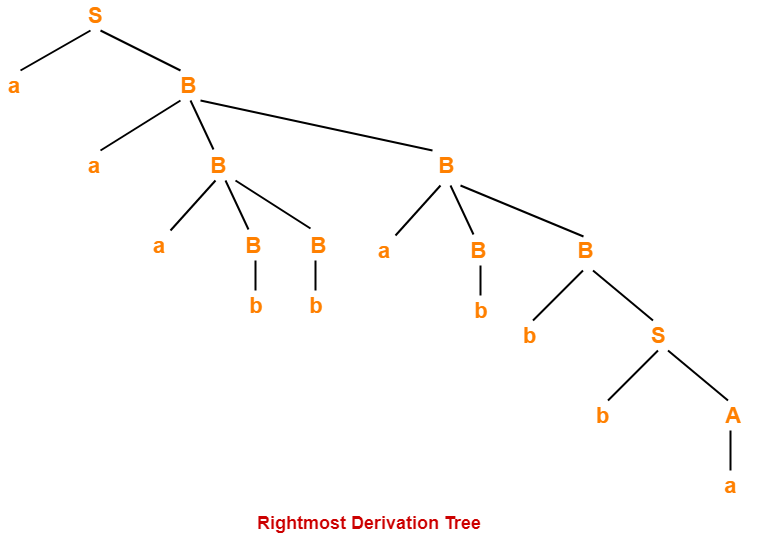
Please refer here for more help!





