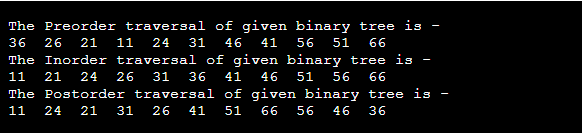
Tree traversal means traversing or visiting each node of a tree.
Linear data structures like Stack, Queue, linked list have only one way for traversing, whereas the tree has various ways to traverse or visit each node. The following are the three different ways of traversal:
- Inorder traversal
- Preorder traversal
- Postorder traversal
Inorder Traversal
An inorder traversal is a traversal technique that follows the policy, Left Root Right.
Let’s understand the inorder traversal through an example.
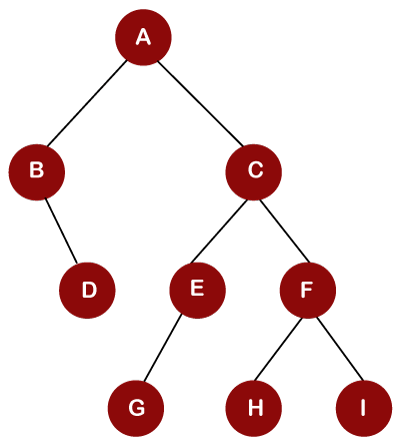
Consider the below tree for the inorder traversal.
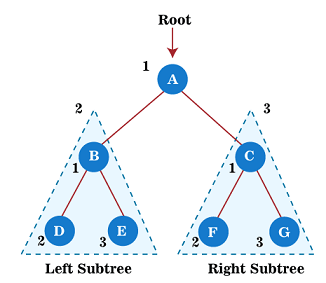
First, we will visit the left part, then root, and then the right part of performing the inorder traversal. In the above tree, A is a root node, so we move to the left of the A, i.e., B.
After visiting node B, we move to the right child of node B, i.e., D.
We move to the right child of node A, i.e., C. The node C has also left child, i.e., E and E has also left child, i.e., G.
The root node of G is E.
Since E does not have any right child, so we move to the root of the E node, i.e., C.

We move to the node F and node F has a left child, i.e., H.

Now we move to the root node of H, i.e., F

After visiting the F node, we move to the right child of node F, i.e., I,

Therefore, the in order traversal of the above tree is B, D, A, G, E, C, H, F, I.
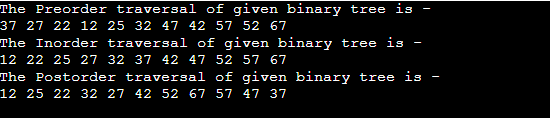
Preorder Traversal
A preorder traversal is a traversal technique that follows the policy, i.e., Root Left Right. Here, the Preorder name itself suggests that the root node would be traversed first.
Let’s understand the Preorder traversal through an example.
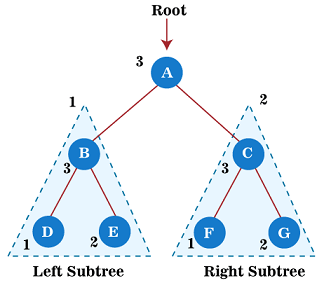
Consider the below tree for the Preorder traversal.
To perform the preorder traversal

In the left subtree, B is the root node for its right child, i.e., D.

Since node B does not have a left child, and it has only a right child;

The right child of node A is C. Since C is a root node for all the other nodes;

Now we move to the left child, i.e., E of node C. Since node E is a root node for node G;

The node E has a left child, i.e., G,

The right child of node C is node F. The node F is a root node for the nodes H and I;

we will traverse the left child, i.e., H of node F

Now we will traverse the right child, i.e., I of node F, as shown below:

Therefore, the preorder traversal of the above tree is A, B, D, C, E, G, F, H, I.
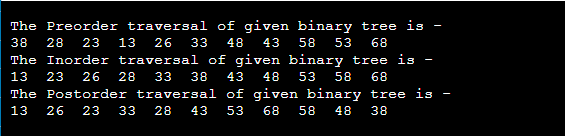
Postorder Traversal
A Postorder traversal is a traversal technique that follows the policy, i.e., Left Right Root. Here, the Postorder name itself suggests that the root node of the tree would be traversed at the last.
Let’s understand the Postorder traversal through an example.
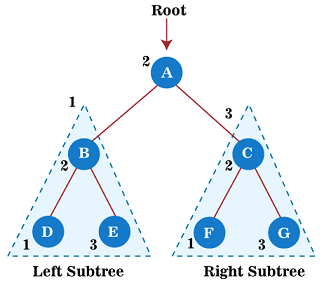
Consider the below tree for the Postorder traversal.
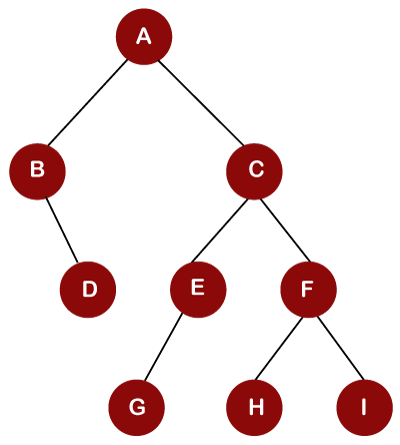
In the above tree, we move to the left child, i.e., B of node A. Since B is a root node for the node D;

We move to the right child of node A, i.e., C. The node E is a root node, and node G is a left child of node E;

The right child of node C is node F. Since F is also a root node for the nodes H and I;

After traversing H and I, node F

Once the right part of node C


Therefore, the Postorder traversal of the above tree is D, B, G, E, H, I, F, C, A.