Heat and work are the forms of energy , in the previous post we had discussed about the work transfer.
The form of energy which flows due to the temperature difference is heat and they phenomenon of its flow is heat transfer .
Heat transfer is :
- Path function
- Boundary phenomenon
- Transient phenomenon
- Not a property of a system
- Inexact differential
- Cyclic integral is non zero
Heat transfer is always written in form :
∆Q ( ✓)
dQ (×), bcoz heat transfer is Inexact differential.
Heat Capacity : ( C )
The amount of heat required to raise the temperature of system by unit degree is heat capacity and it is denoted by C .
C = ∆ Q / ( dT)
∆ Q= C × dT
OR
∆ Q = CdT
C is a coefficient called heat capacity it’s magnitude depends upon:
- Size of the system
- State of the system
- Composition of the system
Unit of C = KJ/ kelvin.
Specific heat : (c)
It is amount of required to rise the temperature of unit mass of substance by one unit .
It is denoted by c ( small alphabet).
Unit of c = KJ/ (Kg – kelvin)
c= ∆ Q / ( M .dT)
∆ Q= M c × dT
∆ Q = McdT
Here ,
∆Q = amount of heat .
M = mass of substance
c = specific heat
C = heat capacity
dT = change in temperature
As we know that the amount of heat is path function , therefore specific heat is also a path function and therefore depend on the constant volume and constant pressure conditions , that helps in defining the path of the system.
Therefore ,
There are two types of specific heat :
(a) cp = specific heat at constant pressure
(b) cv = specific heat at constant volume
These two specific heats have a relationship which is called Meyer’s Relationship , and it valid only for :
(a) unit mass
(b) ideal gas
cp– cv = R
For Heat capacity Meyer’s Relationship :
CP – CV = R
Here
Cp = heat capacity at constant pressure
Cv = heat capacity at constant volume
And from the Meyer’s Relationship it is clear that the
Cp >Cv
Ratio of Cp / Cv :
The ratio of cp / cv is called specific heat ratio and is denoted by ¥ ( gamma)
¥ = specific heat ratio
| Gas | ¥ |
| Triatomic | 1.33 |
| Diatomic | 1.4 |
| Monoatomic | 1.67 |
Sensible heat –
The amount of heat required by any thermodynamic system to change the temperature of the substance is Sensible heat .
Latent heat –
The amount of heat required by the system or a body to change its phase without any interference in temperature is Latent heat .
Therefore , the specific heat of phase change is infinity.
Because , dT = 0 ;
Therefore , c ~ infinity.
For example :
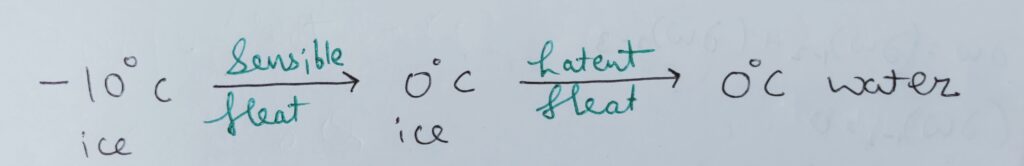


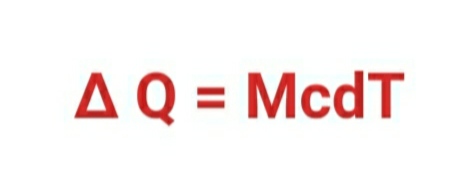

![[Free] Thermodynamics Course With Certification Thermodynamics](https://mechomotive.com/wp-content/uploads/2021/01/SAVE_20210121_225241-218x150.jpg)