MINER’S EQUATION AND FLUCTUATING LOAD STUDY

MINER’S EQUATION : INTRODUCTION TO CUMULATIVE DAMAGE IN FATIGUE

MINER’S EQUATION :Till now, we dealt with stresses that acted on the system in a single stress cycle. In practical analysis, especially in high stress applied tasks, the stress acts in PARTICULAR levels.

Here, a particular mechanical component gets subjected to different stress levels , AND each stress level acting at different parts of the work cycle.

So, MINER developed an EQUATION in order to solve this problem.

The above equation finds use in these stress cycle cases.

MINER’S EQUATION : FORMULA AND IT’S STUDY

Suppose we take a component ; subjected to various completely reversed stresses , each stress cycle acting for various no. of work cycles.

Now, suppose no. of cycles (n₁,n₂,n₃,……) at respective stress levels (σ₁,σ₂,σ₃,……) are unknown.

SOLVED NUMERICAL :

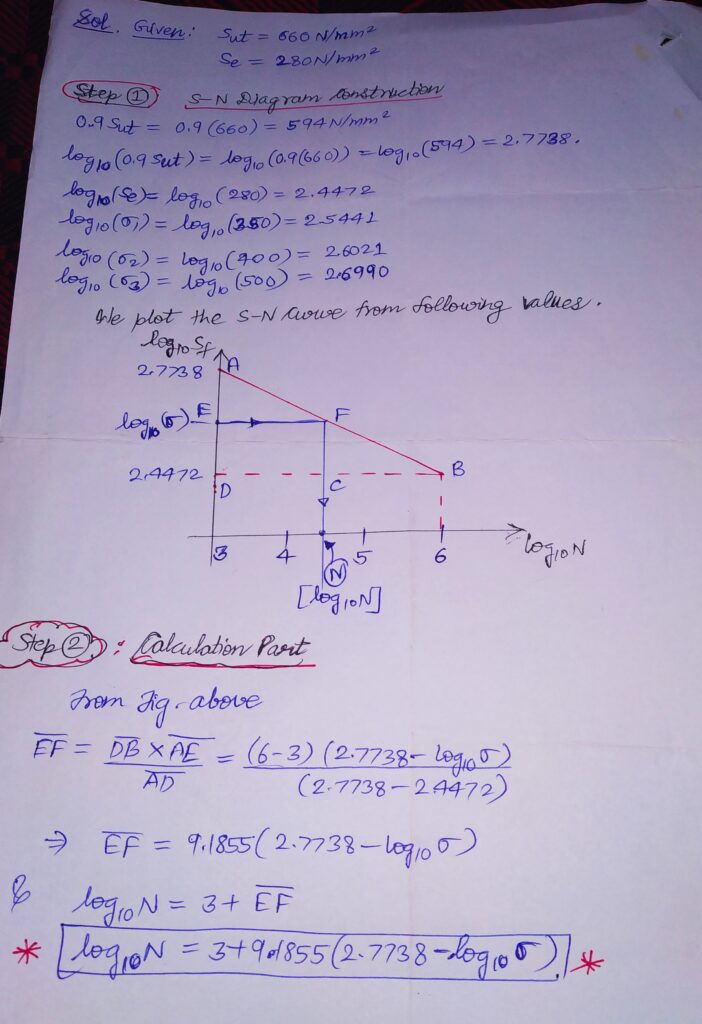
Q1. The work cycle of a mechanical component subjected to completely reversed bending stresses consists of the following three elements;

1) ±350 N/mm² for 85% of time

2) ±400 N/mm² for 12% of time

3) ±500 N/mm² for 3% of time

Material and component is 50C4( S_ut=660 N/mm²) and corrected endurance limit of the component =280 N/mm².

Determine the life of the component.

THEORIES OF FAILURE (DYNAMIC LOADING):

For static loading , we learnt about 5 Theories of Failure (T.O.F) for designing in complex stress systems.

IF NOT SEEN TILL NOW, PLZ REFER TO THE LINK BELOW:

THEORIES OF FAILURE 2 : COMPLEX STRESS

MORE BLOGS CAN BE VIEWED AT http://mechomotive.com/ .

But in fluctuating loading stress systems, design is quite different from others.

Fluctuating loading stresses : Those stresses which have different magnitude of stresses and also induces in a specific direction.

σ_m= σ₁ +σ₂/2  &  σ_{v =} σ₁ – σ₂/2  where , σ₁= maximum stress σ₂= minimum stress

Here, we observed that MEAN STRESS {σ_m} component shows effect on the fatigue failure of a system when present in combination with alternating component.

So, we defined a set THEORIES OF FAILURE (TOF) for the fatigue loading systems.

The criteria for defining TOF for fatigue loading is mainly focused on S N curve characteristics.

S N CURVE CHARACTERISTICS STUDY (STATIC AND FATIGUE):

IN THIS ANALYSIS, we plot MEAN STRESS (σ_m) on x-axis (abscissa) and STRESS AMPLITUDE (σ_a) on y-axis (ordinate).

*** If σ_a=0 ; load is purely static and Criterion is either (S_yt/σ_yt) or (S_ut/σ_ut). These limits plotted on the abscissa.

*** If σ_m=0 ; load is completely reversing and Criterion is Endurance limit (S_e/σ_e) .This point plotted on the ordinate.

*** But when both are present ; σ_a & σ_m and are non zero, The actual failure is impossible to find out. And, the failure usually appears as different scattered points as shown in the figure.

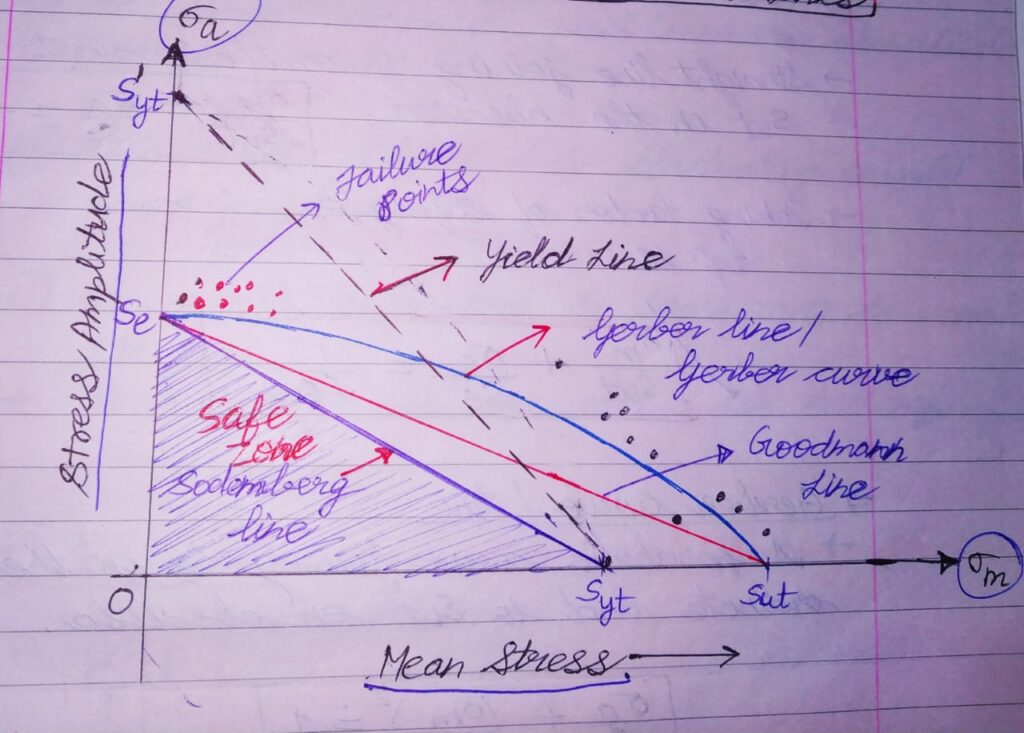
There exists a border in this graph .This border separates safe region from unsafe region for various combinations of σ_a & σ_m.

Different criterions came in existence to derive this safe region characteristics and these all in combination came to be known as “THEORIES OF FAILURE FOR FATIGUE LOADING”.

THEORIES OF FAILURE FOR FATIGUE LOADING kept for discussion in the next blog.

.