NUMERICAL ON HELICAL SPRINGS (COMPRESSION):

NUMERICAL: (APPROACH TO SOLVE PROBLEMS)-

Numerical related to Helical Compression Springs should be done with proper designing procedure. This procedure involves various factors such as to find values corresponding to the given questions and applying Load Stress and Load Deflection Equations.

So as to know more about LOAD-STRESS & LOAD-DEFLECTION EQUATIONS; Plz refer to the link of blog given below and study it thoroughly.

EQUATIONS FOR HELICAL SPRING DESIGN:STUDY

Numerical 1:

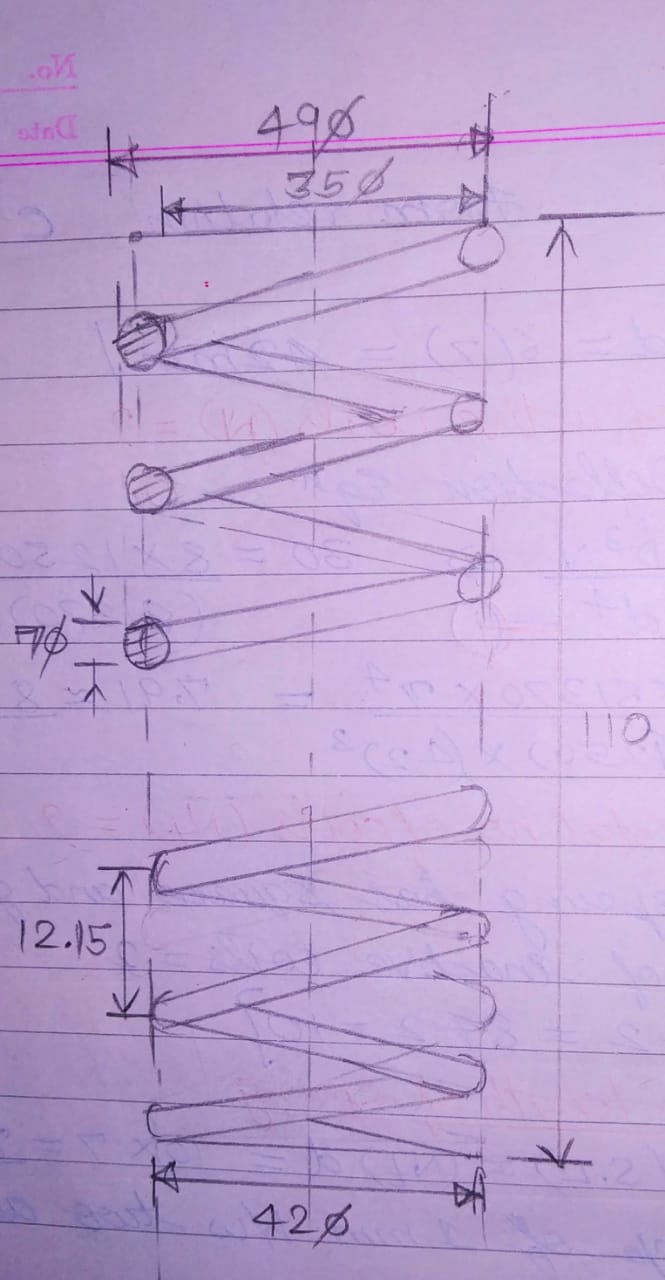
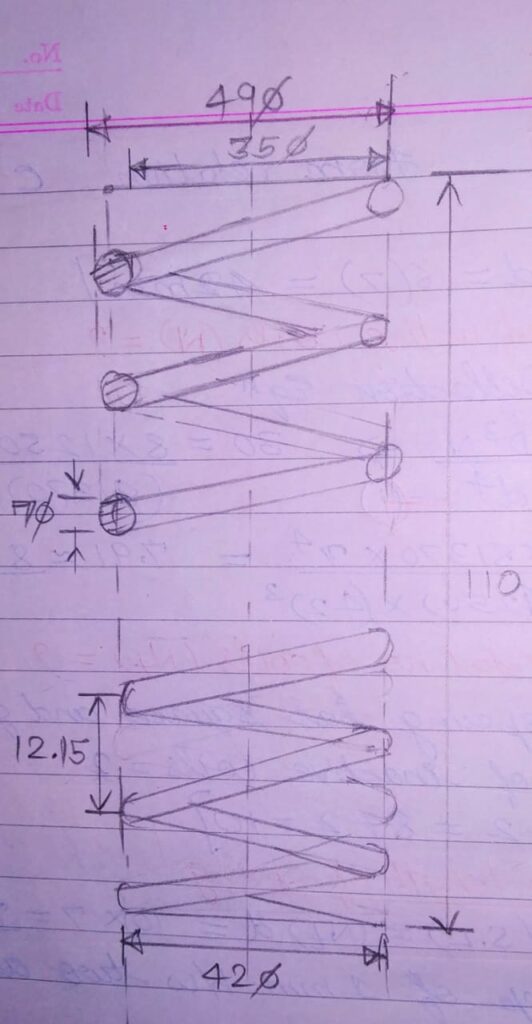
To design a Helical compression spring(H.C.S), subjected to a Max. force of 1250 N. The deflection of spring corresponding to Max. force should be approximate 30 mm. The Spring Index(C)=6. Spring made of Patented and Cold drawn steel wire of Grade1. The constants ( A=1753, m=0.182, G=81370 N/mm²) given as shown. Permissible Shear stress for spring wire taken as 50% of the Ultimate tensile strength (S_ut). Find The following ;

1) Wire diameter(d)

2) Mean Coil diameter (D)

3) No. of active coils (N)

4) Total no. of coils (N_t)

5) Free length of the coils

6) Pitch of coil (p)

Also Design the spring and draw it.

Num. 2:

A Helical compression spring(H.C.S), subjected to a force ranging from 1000 N to 2000 N. The deflection of spring corresponding to this range should be approximate 5 mm. The Spring Index(C)=5. Spring has square and grounded ends. Spring made of Patented and cold drawn steel wire of Grade1. .The constants ( A=1753, m=0.182, G=81370 N/mm²) given as shown. Permissible shear stress for spring wire= 50 % of Ultimate tensile strength (S_ut).

Calculate the following and design the spring:

1) Wire diameter(d)

2) Mean Coil diameter (D)

3) No. of active coils (N)

4) Total no. of coils (N_t)

5) Free length of the coils (F.L)

6) Solid length (S.L)

7) Required spring rate

8) Actual spring rate

Num.3:

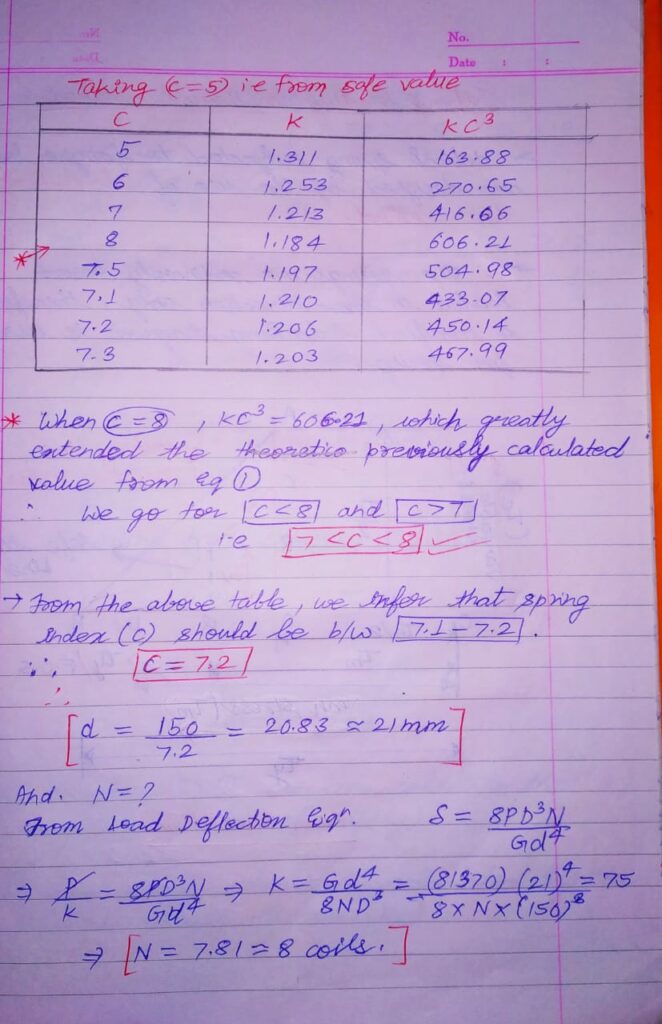
Design a H.C.S with P_max=7.5kN. The mean coil diameter (D) Should be 150 mm from space considerations. k=75 N/mm .Spring made of coil hardened and Tempered steel wire ( S_ut = 1250 N/mm² ). Permissible shear stress= 30 %of Ultimate tensile strength (S_ut). G=81370 N/mm²

Calculate :

1) Wire diameter (d)

2) No. of active coils(N)