Steady flow energy equation and Bernoulli Equation

Steady flow energy equation :

For steady flow energy equation , Consider a control volume, in which mass ∆m1/∆t enters through inlet with parameters

U = internal energy

v = Velocity

V = specific volume ( V₁ = V₂ )

P = pressure

Z= potential head

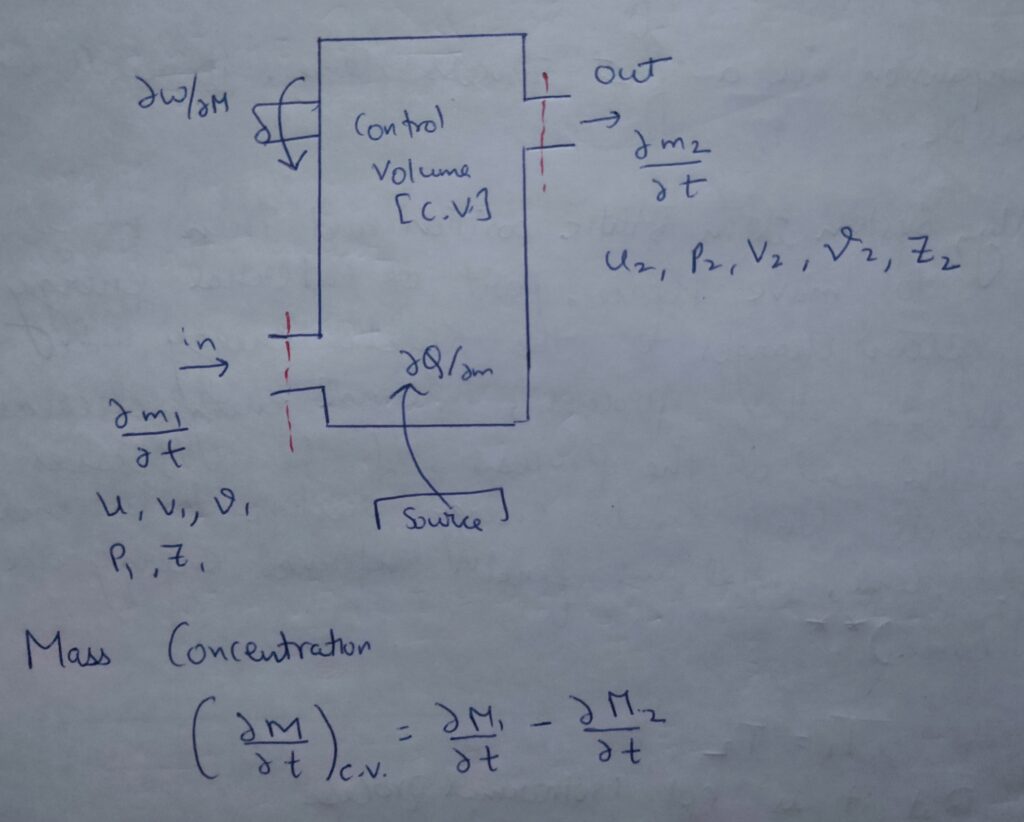
Similarly mass ∆m₂/∆t exits through outlet.

Therefore mass concentrationin control volume is

(∆m/∆t) _{control volume} = ∆m₁/∆t – ∆m₂/∆t

•(∆E/∆t) _in = internal energy+ flow work + kinetic energy+ potential energy + heat

Therefore , (∆E/∆t) _in = ∆m₁/∆t { U₁ + P₁V₁ + v₁²/2 + gZ₁ } + ∆Q/∆t

At exit , (∆E/∆t)_out = ∆m₂/∆t { U₂ + P₂V₂ + v_{2 ²}/2 + gZ₂ } + ∆W/∆t

(E/∆t) _{control volume}= (∆E/∆t)_in – (∆E/∆t)_out

(E/∆t) _{control volume}= ∆m₁/∆t { h₁ + v₁²/2 + gZ₁ } + ∆Q/∆t – ∆m₂/∆t { h₂ + v_{2 ²}/2 + gZ_{2} – ∆W/∆}t

Assumptions :

• (∆m/∆t) _{control volume} = 0

• (E/∆t) _{control volume}= 0

Here , (∆m/∆t) _{control volume} = ∆m₁/∆t – ∆m₂/∆t = 0

So , ∆m₁/∆t = ∆m₂/∆t = m

Similarly,

(∆E/∆t)_in = (∆E/∆t)_out

Therefore ,

m{ h₁ + v₁²/2 + gZ₁ } + ∆Q/∆t = m{ h₂ + v_{2 ²}/2 + gZ₂ } + ∆W/∆t

this is Steady flow energy equation or SFEE .

Bernoulli Equation :

from Steady flow energy equation

m{ h1 + v12/2 + gZ1 } + ∆Q/∆t = m{ h2 + v2 2/2 + gZ2 } + ∆W/∆t

Assume ,

(a)No heat transfer

(b) No work transfer

(c)No change in internal energy

(d)No change in density ( p = constant)

Then ,

m{ h1 + v12/2 + gZ1 } + ∆Q/∆t = m{ h2 + v2 2/2 + gZ2 } + ∆W/∆t

and

U₁ + P₁V₁ + v₁²/2 + gZ₁ = U₂ + P₂V₂ + v_{2 ²}/2 + gZ₂

As , Specific Volume = 1/ Density

i.e., V = 1/ p

Therefore

P₁/p + v₁ ²/2 + gZ₁ = P₂ /p+ v_{2 ²}/2+ gZ₂

P₁/pg + v_{1 ²}/2g + Z₁ = P₂ /pg+ v₂²/2g+ Z₂

This is Bernoulli Equation

Conclusion :

Hence both Steady flow energy equation and Bernoulli Equation are based on energy conservation and Bernoulli Equation is limited form of steady flow energy equation .

This is also known as the first law of thermodynamics for open system.