P-V diagram for different thermodynamic process :

The P-V diagram or pressure volume diagram or pressure volume loop makes the comparative study of thermodynamic variables very simple.

The P-V diagram is very useful to study the changes taking place in one component corresponding to another component.

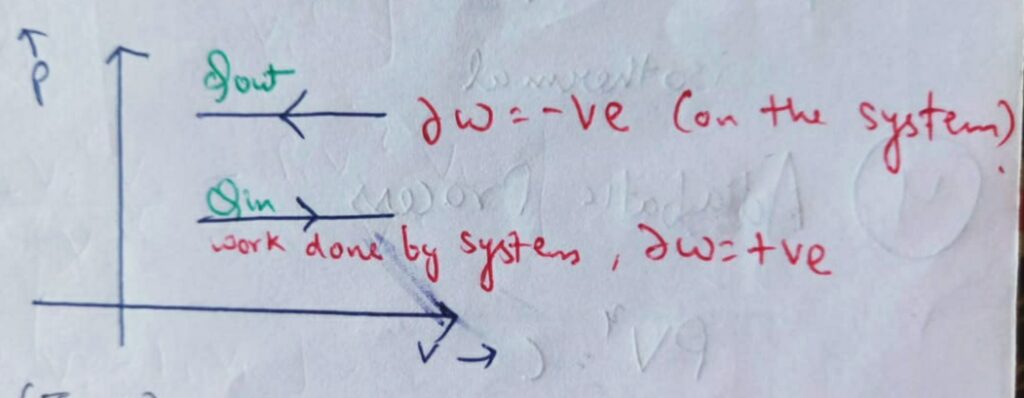
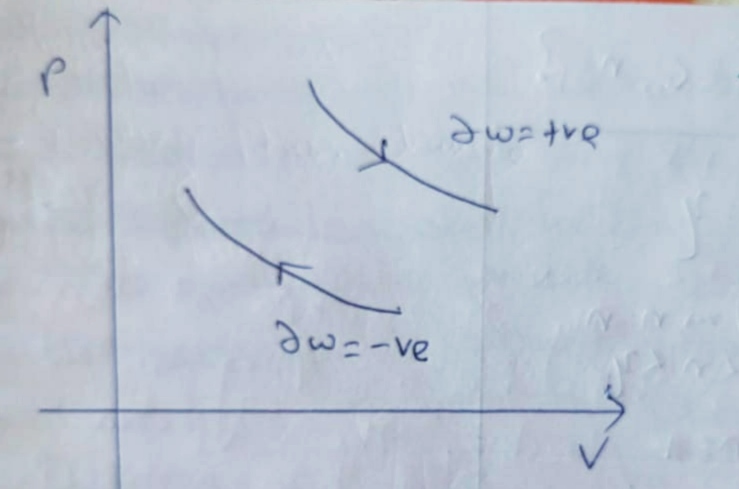
Area under the P-V diagram represents the net work transfer in any thermodynamic process.

P-V diagrams for the different thermodynamic processes are given below :

We have discussed about various thermodynamic processes and their displacement work in the previous post

(a) Isochoric Process :

As we know that in an Isochoric process , volume remains constant ;

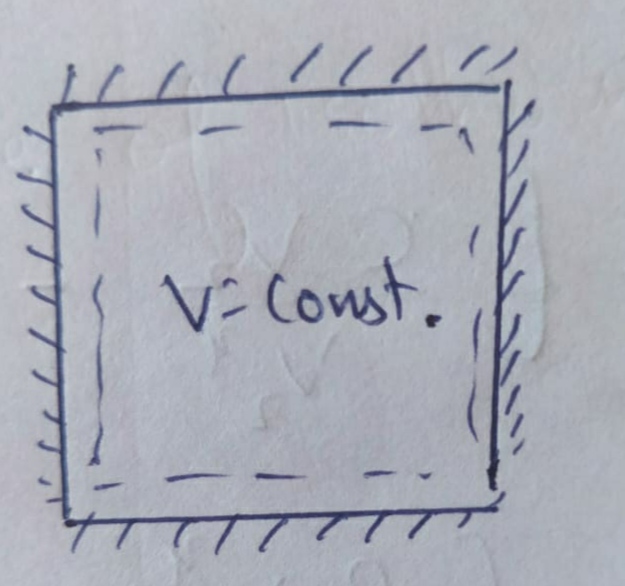
Therefore , PV diagram for Isochoric Process will be straight line.

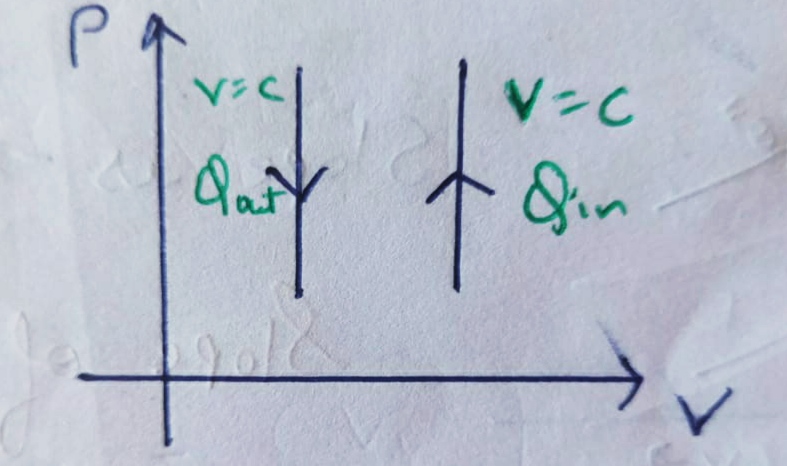
and from it we can conclude that the change in Volume is zero , therefore it’s work done will also be zero.

(b) Isobaric Process :

In the Isobaric Process , presure remains constant ;

And therefore the P-V diagram of Isobaric Process will be straight line with slope zero .

(c) Isothermal process:

In the Isothermal process, the temperatute remains constant ;

i.e., T = constant

Therefore ,

PV = MRT

PV = c ___________eq (1)

Differentiating the above equation , we get

PdV + VdP = 0

OR , PdV = -VdP

(dP/dV ) = -(P/V )

Here we can see that the slope of the PV diagram of Isothermal process is negative.

Therefore it’s PV diagram will be like:

Note : Slope of isothermal process is always negative .

(d) Adiabatic process :

In the Adiabatic process, the net heat transfer is zero ;

and PV^¥ = constant ( here ¥= gamma = adiabatic index)

On differentiating the above equation

We get ,

(dP/dV ) _adiabatic = ¥ ( – P/V )

Here , we can see that the slope of Adiabatic process is also negative but greater in magnitude than that of isothermal process .

Because ¥ >1

Therefore it’s P-V diagram will be like :

(e) Polytropic process :

The Polytropic process obeys the following relation :

PVⁿ = C

Where ,

P = pressure

V = Volume

N = polytropic index

C = constant

On differentiating the above equation , we get

(dP/dV) _Polytropic = N ( -P/ V )

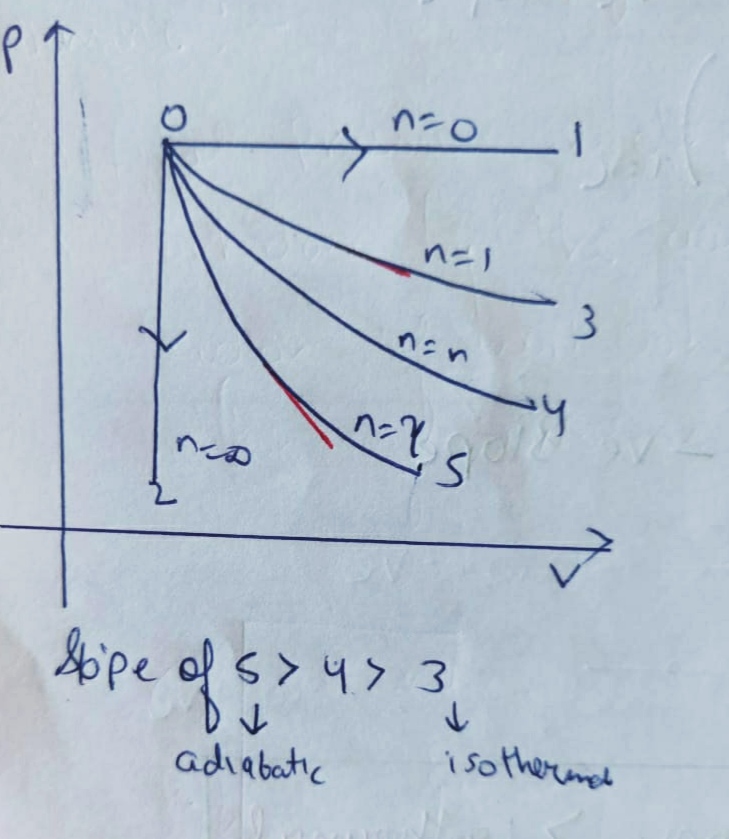
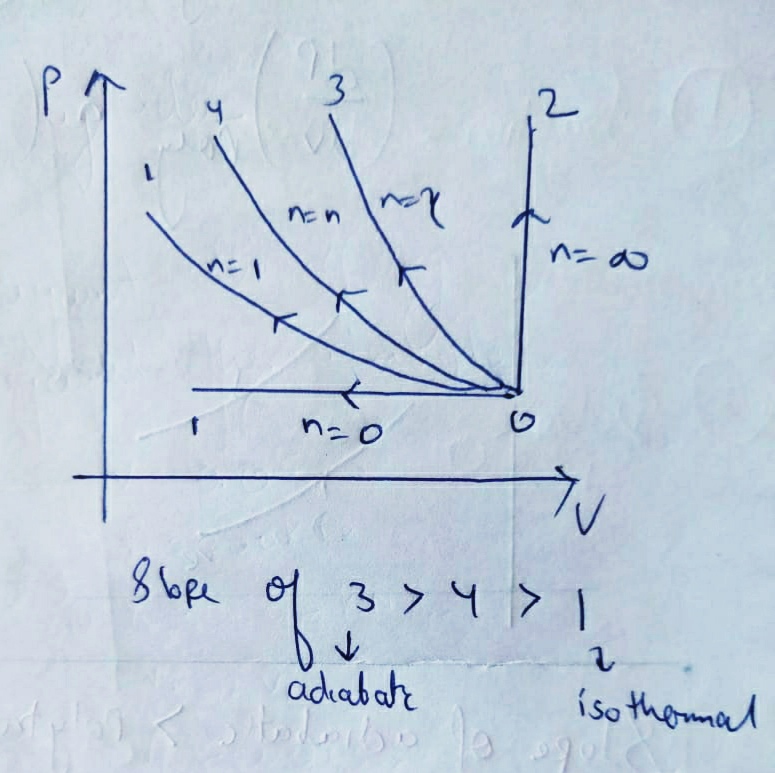
here , we can conclude that the slope of PV diagram of Polytropic process is negative and greater than isothermal process but less than Adiabatic process.

Because , 1 < N < ¥

Therefore the P-V diagram of Polytropic process will be like :

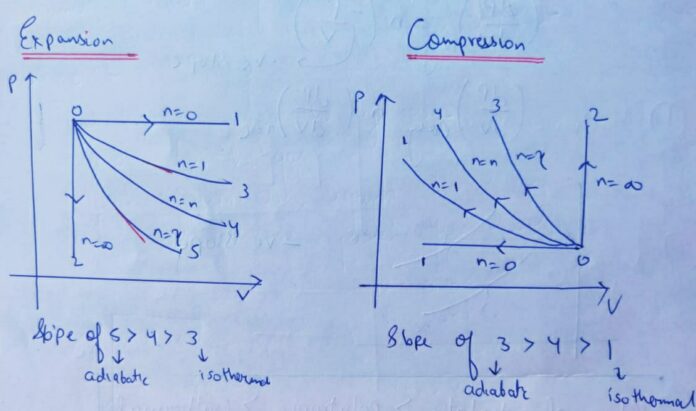
Relationship between Slope of P-V diagram of different thermodynamic processes :

Slope of Adiabatic

>

Polytropic

>

ISOTHERMAL

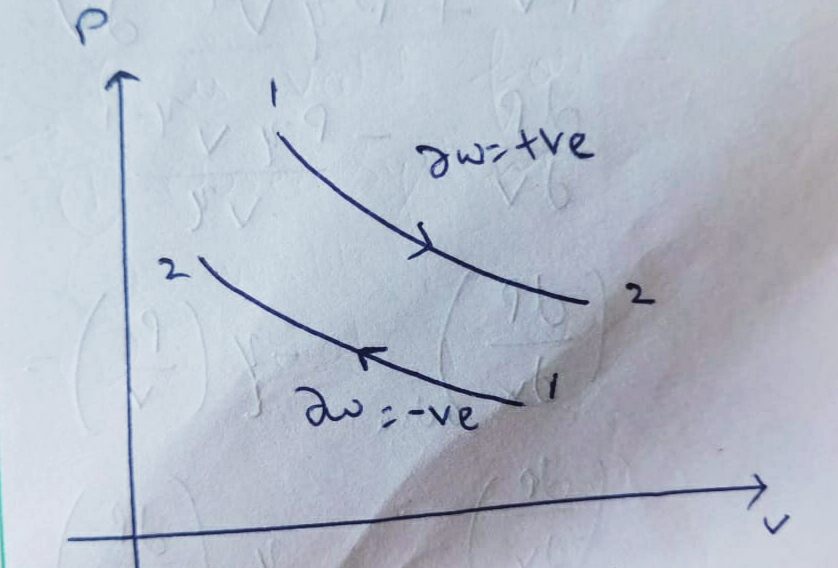
Expansion :

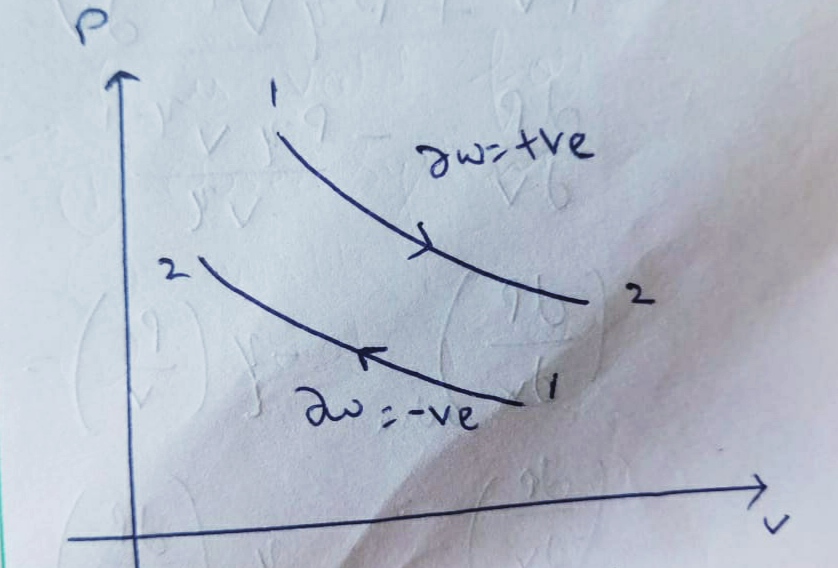
Compression :