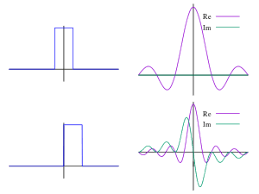
Fourier transform is a mathematical transform that decomposes functions depending on space or time into functions depending on spatial or temporal frequency, such as the expression of a musical chord in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time.
The Fourier transform of a function of time is a complex-valued function of frequency, whose magnitude (absolute value) represents the amount of that frequency present in the original function, and whose argument is the phase offset of the basic sinusoid in that frequency. The Fourier transform is not limited to functions of time, but the domain of the original function is commonly referred to as the time domain. There is also an inverse Fourier transform that mathematically synthesizes the original function from its frequency domain representation, as proven by the Fourier inversion theorem.
Linear operations performed in one domain (time or frequency) have corresponding operations in the other domain, which are sometimes easier to perform. The operation of differentiation in the time domain corresponds to multiplication by the frequency, so some differential equations are easier to analyze in the frequency domain. Also, convolution in the time domain corresponds to ordinary multiplication in the frequency domain.
What is Fourier transform formula?
The Transform is a mathematical technique that transforms a function of time, x(t), to a function of frequency, X(ω). As before, we write ω=nω0 and X(ω)=Tcn. … A little work (and replacing the sum by an integral) yields the synthesis equation of the Transform.
What is difference between Fourier series and Fourier transform?
The Fourier series is use to represent a periodic function by a discrete sum of complex exponentials, while the transform is then use to represent a general, non-periodic function by a continuous superposition or integral of complex exponentials.
Why Fourier transform is use in communication?
In the theory of communication a signal is generally a voltage.And Fourier is essential mathematical tool which provides us an inside view of signal and its different domain, how it behaves when it passes through various communication channels, filters, and amplifiers.
Use of FFT?
FFTs are mainly use to visualize signals. However, there are also applications where FFT results are use in calculations. For example, very simple levels of defined frequency bands can calculate by adding them via an RSS algorithm. Another application is the comparison of spectra.
What is K in Fourier transform?
The Fourier of a function of x gives a function of k, where k is the wavenumber. The Fourier of a function of t gives a function of ω. Where ω is the angular frequency: f˜(ω) = 1. 2π∫−∞.
How do you solve a Fourier transform?
The function F(ω) is call as the transform of the function f(t). Symbolically we can write F(ω) = F{f(t)}. f(t) = F−1{F(ω)}.
What is Fourier series?
A Fourier series is an expansion of a periodic function in terms of an infinite sum of sines and cosines. Fourier Series makes use of the orthogonality relationships of the sine and cosine functions.
What is the relationship between Fourier transform and FFT?
In simple terms, it establishes a relationship between the time domain representation and the frequency domain representation. Fast Fourier , or FFT, is a computational algorithm that reduces the computing time and complexity of large transforms. FFT is just an algorithm used for fast computation of the DFT.
What is the difference between Laplace and Fourier transform?
Laplace transform is normally used for system Analysis, where as transform is used for Signal Analysis. The transform does not really care on the changing magnitudes of a signal. Whereas the Laplace transform ‘care’ both the changing magnitudes (exponential) and the oscillation (sinusoidal) parts.