INFINITE AND FINITE LIFE- NUMERICALS

INFINITE AND FINITE LIFE: APPLICATIONS THROUGH NUMERICALS

Infinite and Finite life numericals along with its analysis play important role in designing process.

So, in this blog, here are some solved examples based on infinite and finite life.

In case you don’t know about INFINITE LIFE AND FINITE LIFE and its concepts, refer to the link given in the link below:

https://mechomotive.com/wp-admin/post.php?post=3823&action=edit

SOME IMPORTANT RELATIONS AND FORMULAE:

Let, S_se = Endurance limit (E.L) of a component subjected to torsional shear stresses

S_e= E.L of a component subjected to reversed bending stresses

(S_e)_a= Value of E. L of a component subjected to axial loading induced stresses.

The relations are :

S_se= 0.5 S_e {MAX.SHEAR STRESS THEORY}

S_se=0.577 S_e {DISTORTION ENERGY THEORY}

(S_e)_a=0.8 S_e {most important relation, keep in mind}

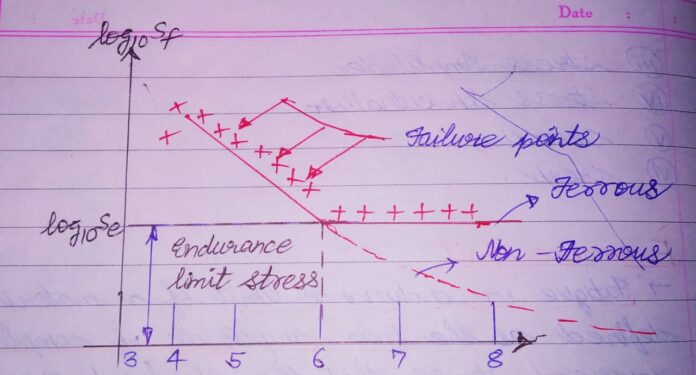
QUESTIONS ON INFINITE LIFE:

Here, the failure criterion is ENDURANCE LIMIT. The stress amplitude should be lower than that of endurance limit of the component.

Q1. A Plate made of steel 20C8 (S_ut=440 N/mm²) in hot rolled condition as shown in figure. It subjected to a completely reversed axial load of 30kN. The notch sensitivity factor (q) can be taken as 0.8 and expected reliability =90 %. The size factor is 0.85 . The factor of safety is 2. Determine the plate thickness (t) for infinite life.

SOL. Given :P= ±30 kN , S_ut=440 N/mm² , q=0.8 , FOS=2 , R=90% K_b=0.85

TO FIND : t= ?

Q2. A Plate made of steel 45C8 (S_ut=630N/mm²) in machined condition as shown in figure. It subjected to a completely reversed axial load of 50kN. The notch sensitivity factor (q) can be taken as 0.8 and expected reliability =90 %. The size factor is 0.85 . The factor of safety is 2. Determine the plate thickness (t) for infinite life.

SOL. Given :P= ±50 kN , S_ut=630 N/mm² , q=0.8 , FOS=2 , R=90% K_b=0.85

TO FIND : t= ?

QUESTIONS ON FINITE LIFE:

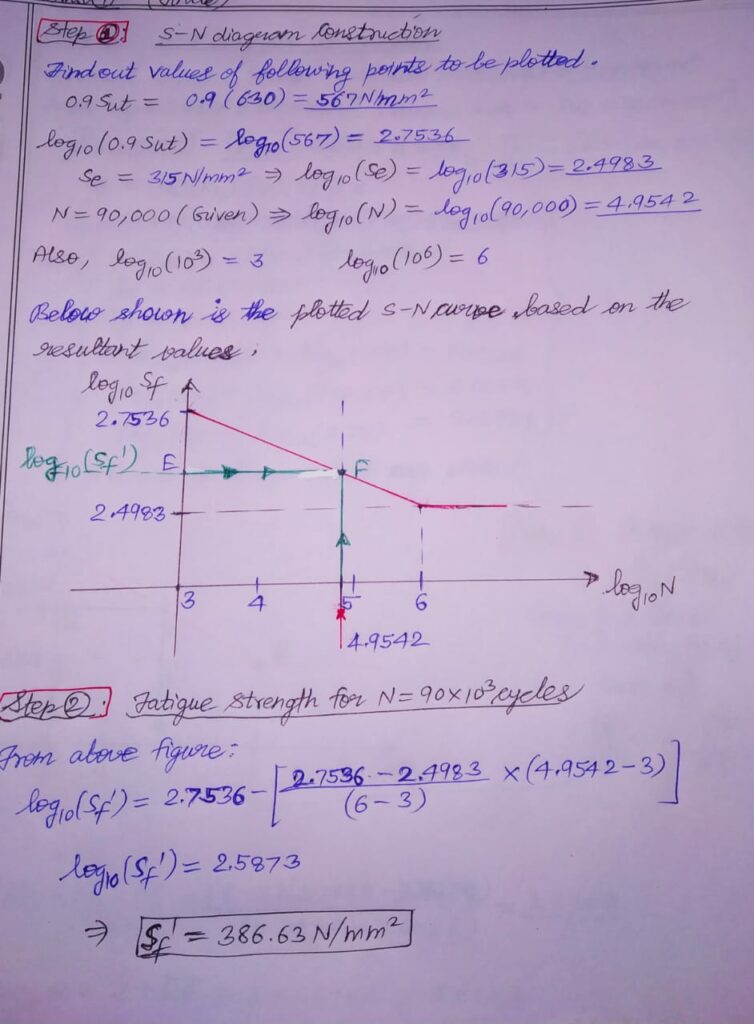
Q1. A rotating bar made of steel 45C8 (S_ut=630 N/mm²) subjected to completely reversed bending stress. The corrected endurance limit of the bar is 315 N/mm². Calculate Fatigue Strength of the bar for a life of 90,000 cycles.

SOL. GIVEN: S_ut=630 N/mm² S_e= 315 N/mm² N=90000

TO FIND : S_f (at 90000 cycles) = ?????

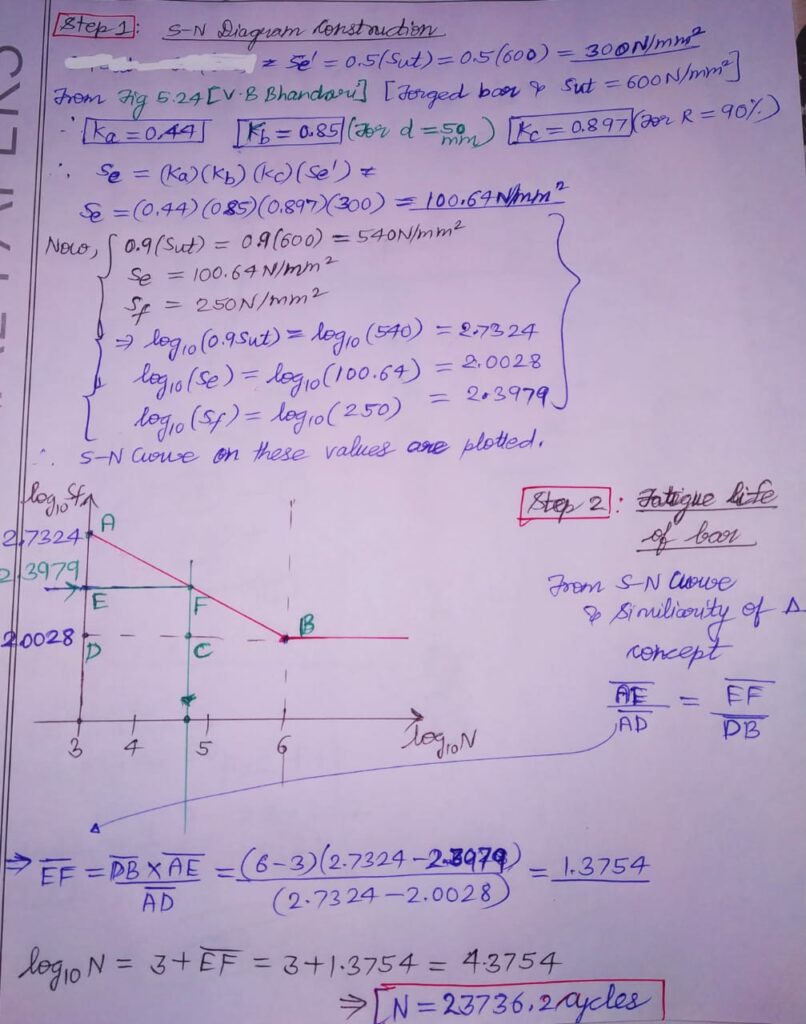
Q2. A forged steel bar, 50 mm in diameter, subjected to a reversed bending stress of 250 N/mm². The bar is made of steel 40C8 (S_ut=600 N/mm²) . Calculate the life of the bar for reliability of 90%.

SOL.GIVEN: S_f= σ_b=250 N/mm² S_ut=600 N/mm² R=90%

TO FIND : N (for S_f=250 N/mm² )= ?????