If you are here, then chances are that you were trying to solve the “Maximum Subarray Problem”. And came across Kadane’s Algorithm but couldn’t figure out how something like that is working. You were tired of using Kadane’s Algorithm as a “black-box”. I wanted to understand the dynamic programming aspect of it. Or maybe you just want to learn about a new concept which make better at programming. As a result the reason, you’ve come to the right place.

Then, we would look at a quite popular programming problem, the Maximum Subarray Problem.
Dynamic Programming
Dynamic Programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems. This is mainly an optimization over plain recursion. Divide & Conquer algorithm partition the problem into disjoint subproblems solve the subproblems recursively. The idea is to simply store the results of subproblems, so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial.
Kadane’s Maximum Subarray Problem
The maximum subarray problem is the task of finding the largest possible sum of a contiguous subarray, within a given one-dimensional array A[1…n] of numbers. For example, for the array given above, the contiguous subarray with the largest sum is [4, -1, 2, 1], with sum 6. We would use this array as our example for the rest of this article.

We assume this array to be zero-indexing, i.e. -2 would be call as the ‘0th’ element of the array.
Brute Force Approach
One very obvious but not so good solution is to calculate the sum of every possible subarray and the maximum of those would be the solution.We can start from index 0 and calculate the sum of every possible subarray starting with the element A[0]. We will call the maximum sum of subarrays starting with element A[i] the local_maximum at index i. Thus after going through all the indices, we would be left with local_maximum for all the indices.
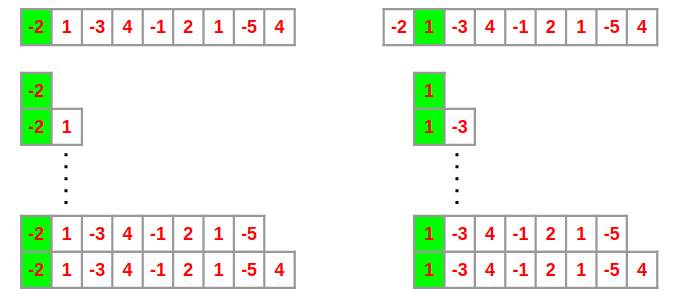
We can find the maximum of these local_maximums and we would get the final solution, i.e. the maximum sum possible. We would call this the global_maximum. Kadane’s algorithm is able to find the maximum sum of a contiguous subarray in an array with a runtime of O(n). This algorithm can be viewed as a simple example of dynamic programming.
Please refer here for more help!





