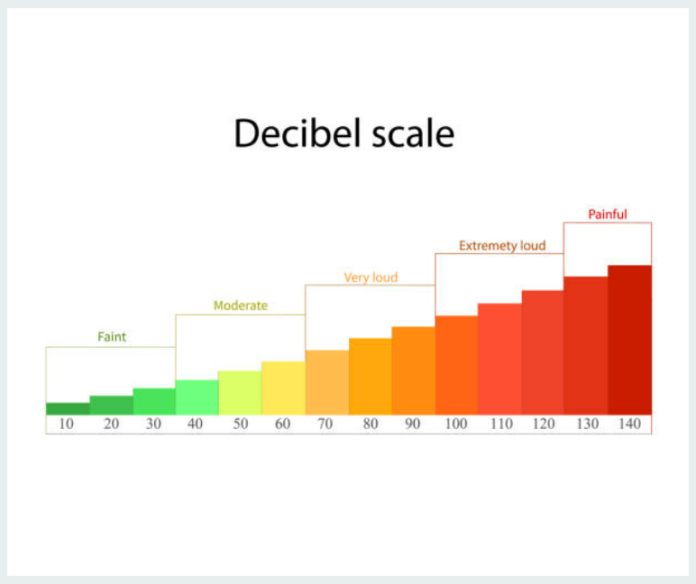
The characteristics of audio signals and noise are often specified in decibel (dB).
The bel is defined as the base ten logarithm of a power ratio.
The logarithm compresses the numerical range of its argument;
This is often a convenient feature when one must deal with numbers differing over several orders of magnitude.
We have,
Logarithm properties
1.log P 1 P 2 = log P 1 + log P 2
2. log P 1 / P 2 = log P 1 – log P 2
3. log P n = n log P
4. log 1 = 0
In communications systems, gain is measured in bels.
The bel is used to measure the ratio of two levels of power or power gain G; i.e.,
G = Number of bels = log 10 (P 2 / P 1 ) …(1)
The decibel (dB) provides us with a unit of less magnitude.
It is 1/10th of a bel and is given by
G dB = 10 log 10 (P 1 / P 2 ) …(2)
When P 1 = P 2, there is no change in power and the gain is 0 decibel (dB). If
P 2 = 2P 1, the gain is
G dB = 10 log 10 2 = 3 dB …(3)
and when P 2 = 0.5P 1 , the gain is
G dB = 10 log 10 0.5 = −3 dB …(4)
Equations (3) and (4) show another reason why logarithms are
greatly used:
“The logarithm of the reciprocal of a quantity is simply negative the logarithm of that quantity.”
Further, the gain G can be expressed in terms of voltage or
current ratio.
To do so, consider the network shown in Fig.
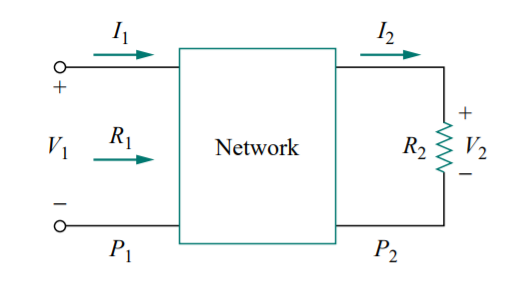
If P 1 is the input power, P 2 is the output (load) power, R 1 is the input resistance,
and R 2 is the load resistance, then P 1 = 0.5V 1 2 /R 1 and P2 = 0.5 V2 2 /R 2 ;
and Eq. (2) becomes
GdB = 10 log 10 P2/P1 = 10 log 10 (V2 2/R2) / (V1 2/R1) …(5)
= 10 log 10 (V2/V 1)2 + 10 log 10 R1/R2
= 20 log 10 (V2/V 1) – 10 log 10 R2/R1 …(6)
Other cases
When R 2= R 1, after comparing voltage levels, Eq. (6) becomes
GdB = 20 log 10 V2/V 1 …(7)
Instead, if P1 = I2 1/R1 and P2 = I2 2/R2, for R1 = R2, we obtain
GdB = 20 log 10 I 2/I 1 …(8)
To know more >> Click here