Quantization, involved in image processing, is a lossy compression technique achieved by compressing a range of values to a single quantum value. When the number of discrete symbols in a given stream is reduced, the stream becomes more compressible. For example, reducing the number of colors required to represent a digital image makes it possible to reduce its file size. Specific applications include DCT data quantization in JPEG and DWT data quantization in JPEG 2000.
The human eye is fairly good at seeing small differences in brightness over a relatively large area, but not so good at distinguishing the exact strength of a high frequency (rapidly varying) brightness variation. This fact allows one to reduce the amount of information required by ignoring the high frequency components. This is done by simply dividing each component in the frequency domain by a constant for that component, and then rounding to the nearest integer. This is the main lossy operation in the whole process. As a result of this, it is typically the case that many of the higher frequency components are rounded to zero, and many of the rest become small positive or negative numbers.
A typical video codec works by breaking the picture into discrete blocks (8×8 pixels in the case of MPEG). These blocks can then be subject to discrete cosine transform (DCT) to calculate the frequency components, both horizontally and vertically. The resulting block (the same size as the original block) is then pre-multiply by the quantize scale code and divided element-wise by the matrix, and rounding each resultant element.
Why do we need quantization?
Quantization, in essence, lessens the number of bits needed to represent information. Lower-precision mathematical operations, such as an 8-bit integer multiply versus a 32-bit floating point multiply, consume less energy and increase compute efficiency, thus reducing power consumption.
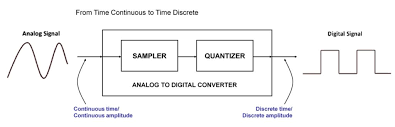
What is quantization resolution?
Quantization error is the difference between the analog signal and the closest available digital value at each sampling instant from the A/D converter. The higher the resolution of the A/D converter, the lower the quantization error and the smaller the quantization noise.
What are the types of quantization?
There are two types of Quantization – Uniform and Non-uniform. The type of quantization in which the quantization levels are uniformly space is termed as a Uniform Quantization.
What is the function of quantizer?
The quantizer allocates L levels to the task of approximating the continuous range of inputs with a finite set of outputs. The range of inputs for which the difference between the input and output. It is small, call the operating range of the converter.
Where does quantization occur during digital image formation?
It is on y axis. When you are quantizing an image, you are actually dividing a signal into quanta(partitions). On the x axis of the signal, are the co-ordinate values, and on the y axis, we have amplitudes. So digitizing the amplitudes is refer as Quantization.
What is the output of quantizer?
When the first input is receive, the quantizer step size is 0.5. Therefore, the input falls into level 0, and the output value is 0.25, resulting in an error of 0.15. As this input fell into quantizer level 0. The new step size is M 0 × Δ 0 = 0.8 × 0.5 = 0.4 .
What is pixel quantization?
This is the process of sampling a continuous tone image to result in a matrix of grayscale values with the coordinates X,Y each with an intensity value of i. The smallest area, usually a square, in a digital image is call as the ‘pixel. Digital images are easy due to this quantization.
What is the quantization interval?
To quantize the samples, the digitization hardware decomposes the range of possible sample values into a finite set of intervals, called quantize intervals. And associates a different binary number with each interval.
How effectiveness of quantization can be improved?
Oversampling reduces the noise power contained within the input signal bandwidth. The equation above shows that for each doubling of the sampling rate relative to the input bandwidth. The theoretical limit on SNR can be increases by 3 dBs, an increase in effective resolution of 1 2 bit.