Factor of stress concentration is necessary in order to enhance safe design of components . It also leads to an increase in efficiency of the production process.
But before the analysis, let’s understand the trend of stress concentration factor in different machine components. We also see how stress concentration factor shows variations according to the geometry of the component.
STRESS CONCENTRATION FACTOR(Kt) – METHODS,VALUES AND VARIATIONS:
METHODS OF FINDING STRESS CONCENTRATION FACTOR:
1. THEORY OF ELASTICITY (WHICH GAVE MATHEMATICAL ANALYSIS)
2.PHOTO ELASTICITY (WHICH GAVE EXPERIMENTAL ANALYSIS)
NOWADAYS, FINITE ELEMENT METHOD {F.E.M} Package has been the most commonly used method.
R.E.PETERSON made several charts plotted by experimental values which came from different geometric shapes as well as loading conditions.
VALUES OF (Kt)- BASED ON DIFFERENT COMPONENTS AND SHAPES
NOTATIONS:
P= LOAD APPLIED W=Width of plate(rectangular)
d= Diameter of hole (in rectangular plate) σo=Nominal stress
= Inner diameter /minor diameter (in all other cases)
D = Outer diameter Mt= Torsional moment I= Moment of inertia
J= Polar Moment of inertia y= Dist. of bending plane from N.A
1. RECTANGULAR PLATE WITH TRANSVERSE HOLE UNDER STRESS DUE TO LOAD:
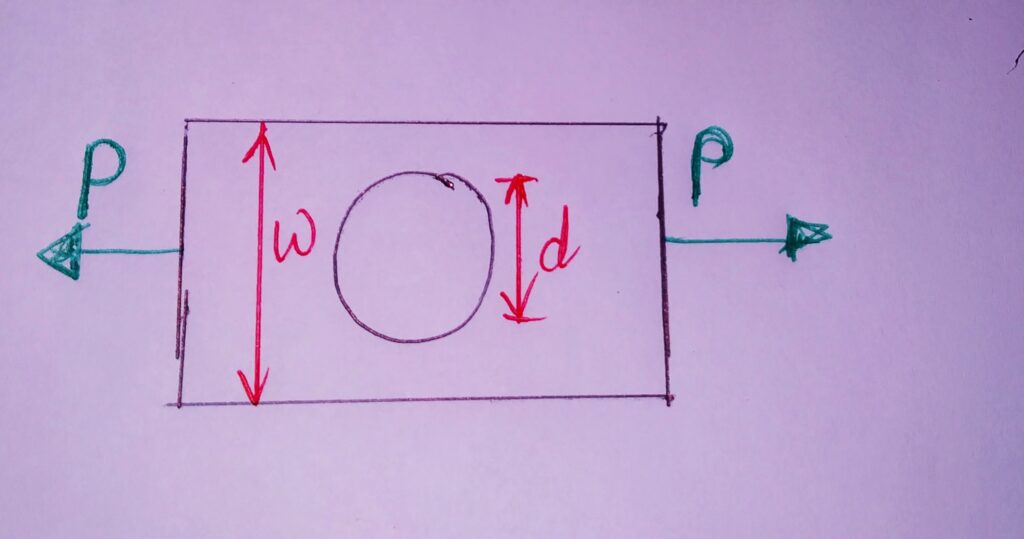
σo = P/(w-d)t where, t= Thickness of plate
2. FLAT PLATE WITH SHOULDER FILLET UNDER STRESS DUE TO AXIAL LOAD :
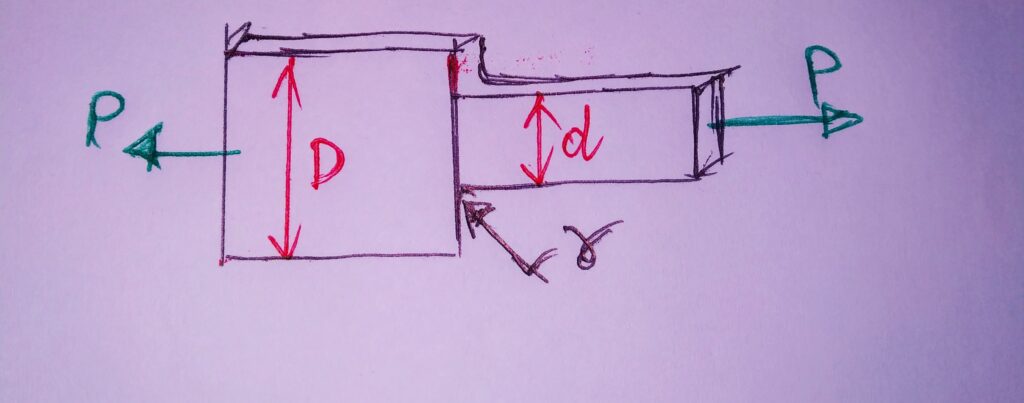
σo = P/(dt) where, t= Thickness of plate
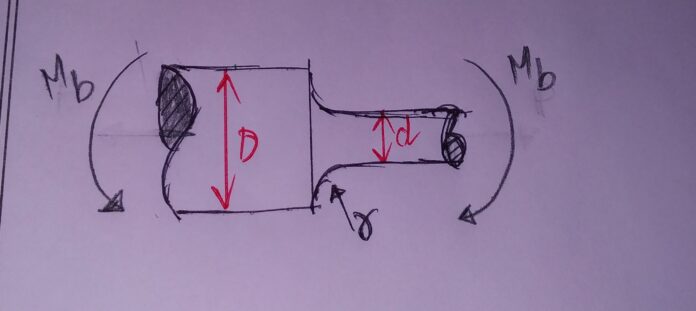
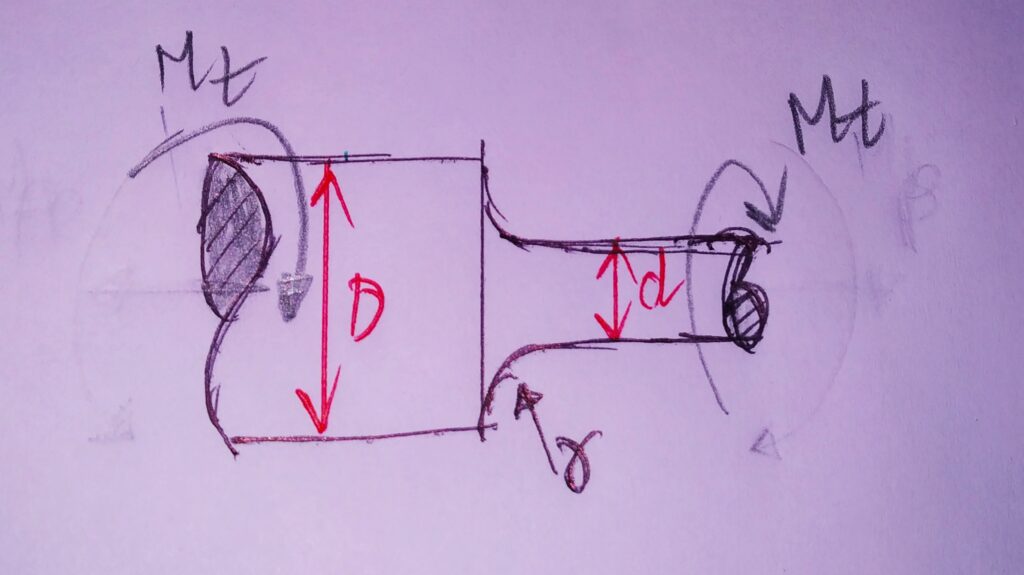
3.ROUND SHAFT WITH SHOULDER FILLET UNDER STRESS:
DUE TO TENSILE FORCE: σo = P/ (Πd2/4)
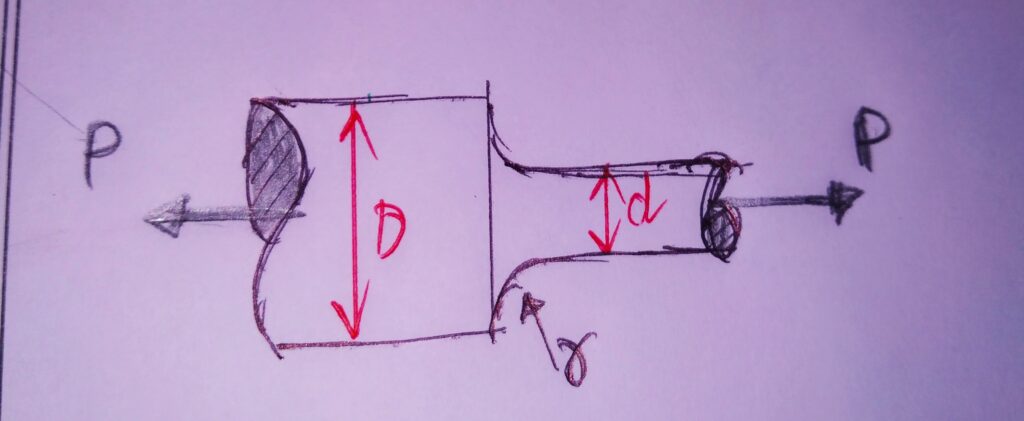
BENDING MOMENT: σ0 = Mb y /I Y=d/2 I=Πd4/64
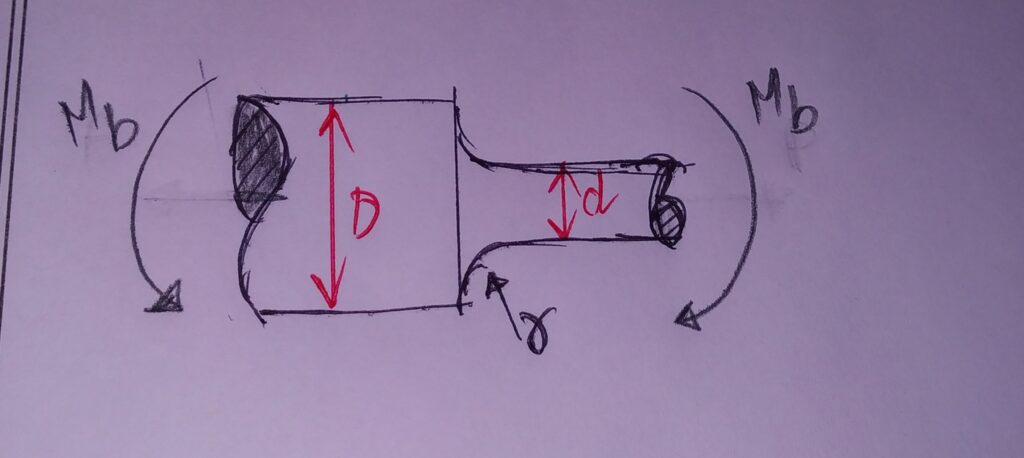
TORSION: τ0 = Mt r /J r=d/2 J = Πd4/32
THEORY OF ELASTICITY- APPLICATION IN FINDING Kt
Some simple geometric shapes can be taken for finding Stress concentration factor (Kt) Using Theory of elasticity.
A flat plate with an elliptical hole subjected to axial load can be taken to find Kt.
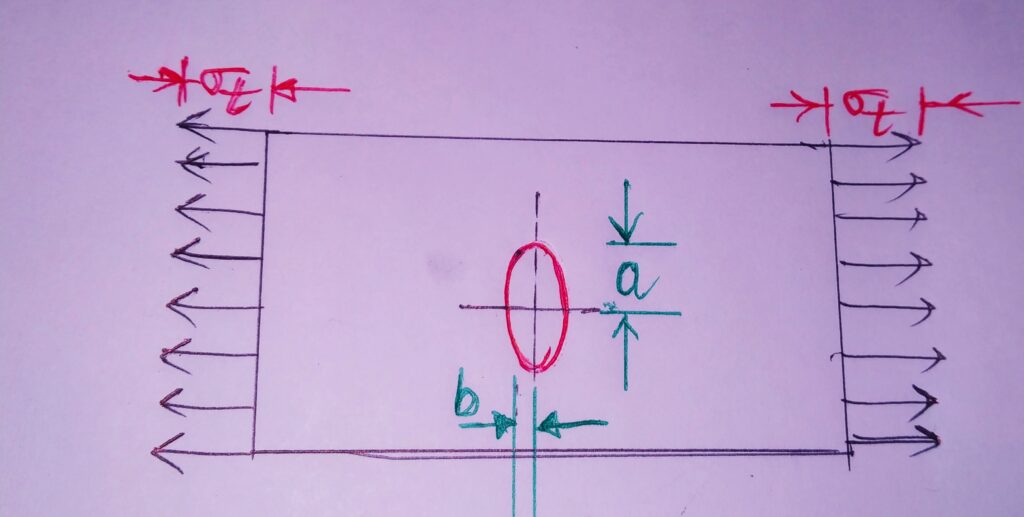
Using Theory Of Elasticity,
Kt=1+2 (a/b)
Where, a= Half width(semi -major axis) of ellipse perpendicular to load direction
b=Half width(semi -minor axis) of ellipse along the load direction
CONDITIONS:
1. b approaches zero (i.e b=0)
Ellipse becomes more and more sharper. Stress at the edge of crack is very high.
Therefore,
Kt=∞ at b=0
2.When a=b
Ellipse becomes circle.
Therefore,
Kt=3 at b=a